✔ 논리연산
논리연산의 개요
2진 디지털 시스템에서 입출력 관계를 표현하는 방법
1. 그래프나 진리표
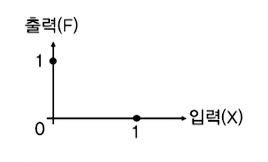
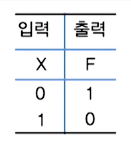
2. 논리함수
입력에 따라 변수가 어떻게 변하는가를 나타내는 함수로 표현
입력이 2진 논리값이므로 논리함수(F = X)로 나타낸다.
논리집합과 논리연산
논리집합(부울집합)
집합이 0(거짓)과 1(참)으로만 구성된 집합 {0,1}
논리연산(부울연산)
두 개의 이산값에 적용되는 연산
논리집합{0,1}에 대한 세 가지 논리연산
- AND 연산 : 점( · )으로 표시, 생략 가능
- OR 연산 : 덧셈 기호(+)로 표시
- NOT 연산 : 변수 위에 줄(-)을 그어 표시
✔ 논리게이트
기본 논리게이트
1. AND 게이트
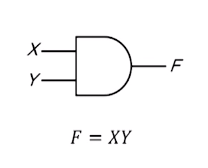
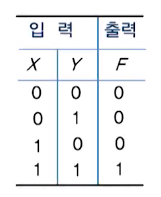
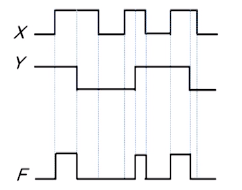
2. OR 게이트
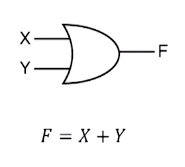
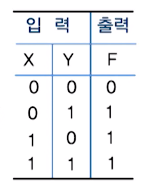
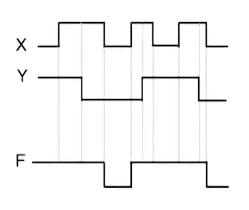
3. NOT 게이트
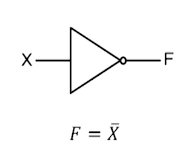
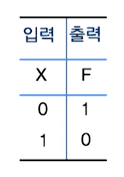

NAND 게이트와 NOR 게이트
1. NAND 게이트
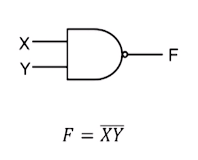
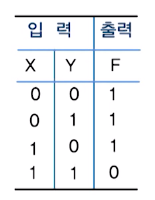
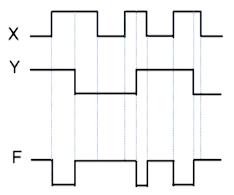
2. NOR 게이트
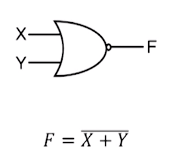
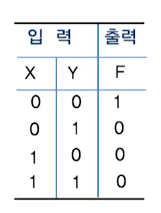
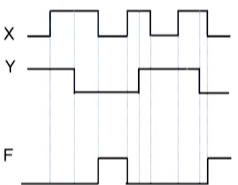
XOR 게이트와 XNOR 게이트
1. XOR 게이트

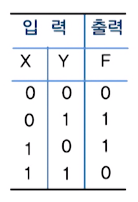
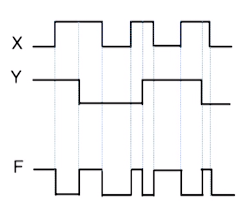
2. XNOR 게이트
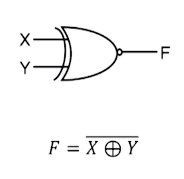
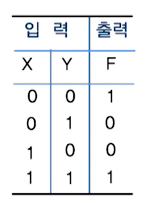
✔ 부울대수
부울대수의 개요
부울대수(Boolean Algebra) : 0과 1의 값을 갖는 논리변수와 논리연산을 다루는 대수
부울함수(Boolean Function) : 논리변수의 상호관계를 나타내기 위해 부울변서, 부울연산기호, 괄호 및 등호등으로 나타내는 대수적 표현
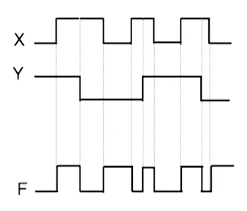
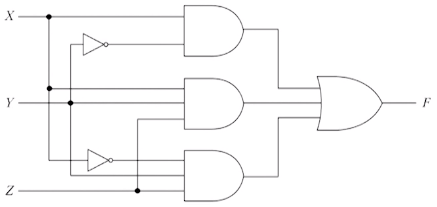
부울함수와 논리회로도
부울함수는 논리 게이트들로 구성되는 논리회로도를 작성 가능

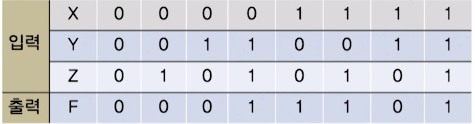
부울함수와 진리표
진리표(truth table) : 논리변수에 할당한 0가 1의 조합 리스트
- 부울함수는 진리표로 나타낼 수 있다.
- 부울함수에 대한 진리표는 하나이다. 그러나 동일 진리표를 만족하는 부울함수는 여러 개가 될 수 있다.
- 따라서 동일 진리표에 대한 논리회로도는 여러 개가 될 수 있다.
- 논리회로도는 단순해야 한다. 복잡하면 게이트 수, 입력 수가 많아지므로 비효율적이다.
- ∴ 부울함수의 단순화(간소화)가 필수
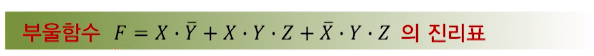
부울함수 간소화의 필요성

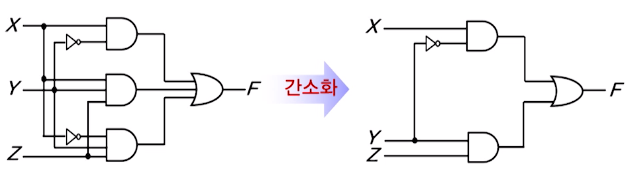
부울함수의 간소화 방법
- 대수적인 방법
- 도표를 이용한 방법
- 테이블을 이용한 방법
기본공식
부울대수의 기본 공식

부울대수의 쌍대성 원리(principle of duality)
부울대수에서 어떤 부울공식이 항상 성립학 자신의 쌍대형태를 구할 수 있다면, 그 쌍대 형태의 부울식도 성립한다.
※ 쌍대형태 : 논리연산자 + 와 · 그리고 논리상수 1과 0을 맞바꾼 형태

부울함수의 대수적 간소화
항 결합

문자 소거
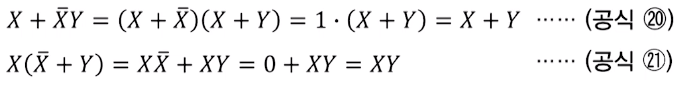
부울함수의 보수
부물함수 F의 보수는 F'
드모르간 정리 : AND와 OR을 서로 바꾸고 각 변수의 보수를 취한다.
✔ 논리연산
논리연산의 개요
2진 디지털 시스템에서 입출력 관계를 표현하는 방법
1. 그래프나 진리표


2. 논리함수
입력에 따라 변수가 어떻게 변하는가를 나타내는 함수로 표현
입력이 2진 논리값이므로 논리함수(F = X)로 나타낸다.
논리집합과 논리연산
논리집합(부울집합)
집합이 0(거짓)과 1(참)으로만 구성된 집합 {0,1}
논리연산(부울연산)
두 개의 이산값에 적용되는 연산
논리집합{0,1}에 대한 세 가지 논리연산
- AND 연산 : 점( · )으로 표시, 생략 가능
- OR 연산 : 덧셈 기호(+)로 표시
- NOT 연산 : 변수 위에 줄(-)을 그어 표시
✔ 논리게이트
기본 논리게이트
1. AND 게이트



2. OR 게이트
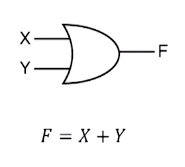


3. NOT 게이트



NAND 게이트와 NOR 게이트
1. NAND 게이트



2. NOR 게이트



XOR 게이트와 XNOR 게이트
1. XOR 게이트



2. XNOR 게이트
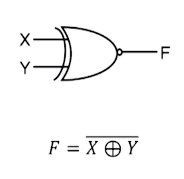


✔ 부울대수
부울대수의 개요
부울대수(Boolean Algebra) : 0과 1의 값을 갖는 논리변수와 논리연산을 다루는 대수
부울함수(Boolean Function) : 논리변수의 상호관계를 나타내기 위해 부울변서, 부울연산기호, 괄호 및 등호등으로 나타내는 대수적 표현
부울함수와 논리회로도
부울함수는 논리 게이트들로 구성되는 논리회로도를 작성 가능


부울함수와 진리표
진리표(truth table) : 논리변수에 할당한 0가 1의 조합 리스트
- 부울함수는 진리표로 나타낼 수 있다.
- 부울함수에 대한 진리표는 하나이다. 그러나 동일 진리표를 만족하는 부울함수는 여러 개가 될 수 있다.
- 따라서 동일 진리표에 대한 논리회로도는 여러 개가 될 수 있다.
- 논리회로도는 단순해야 한다. 복잡하면 게이트 수, 입력 수가 많아지므로 비효율적이다.
- ∴ 부울함수의 단순화(간소화)가 필수
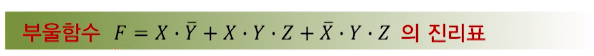

부울함수 간소화의 필요성


부울함수의 간소화 방법
- 대수적인 방법
- 도표를 이용한 방법
- 테이블을 이용한 방법
기본공식
부울대수의 기본 공식

부울대수의 쌍대성 원리(principle of duality)
부울대수에서 어떤 부울공식이 항상 성립학 자신의 쌍대형태를 구할 수 있다면, 그 쌍대 형태의 부울식도 성립한다.
※ 쌍대형태 : 논리연산자 + 와 · 그리고 논리상수 1과 0을 맞바꾼 형태

부울함수의 대수적 간소화
항 결합

문자 소거
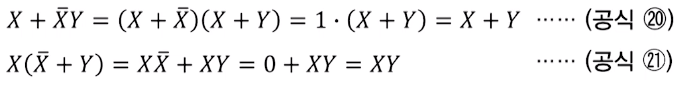
부울함수의 보수
부물함수 F의 보수는 F'
드모르간 정리 : AND와 OR을 서로 바꾸고 각 변수의 보수를 취한다.
