✔ 명제
명제(Proposition) : 참과 거짓을 구별할 수 있는 문장이나 수학적 식
명제의 진리값(truth value)
참(true), T : 명제가 타당한 경우
거짓(False), F : 명제가 타당하지 않은 경우
6은 2의 배수다 : 명제 (진리값이 참)
2, 3, 6은 소수이다 : 거짓 (F)
✔ 논리 연산
합성명제(compund proposition)
하나 이상의 명제와 논리연산자 그리고 괄호로 이루어진 명제
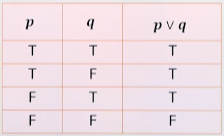
1) 논리합(disjunction; or, ᵛ)
둘 중 하나라도 참이면 진리값은 참이다.
2) 논리곱(conjunction: and, ^)
둘 중 하나라도 거짓이면 진리값은 거짓이다.

3) 부정(negarion; ~, ㄱ)
1항 연산, not

4) 배타적 논리합(exclusive or; xor, ⊕)
둘 다 참인 것을 제외함

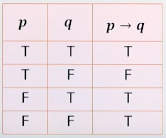
조건명제(conditional proposition, →)
명제 p와 q가 있을 때, 명제 p가 조건의 역할을 수행하고 명제 q가 결론의 역할을 수행하는 경우
p → q
p는 q의 충분조건
q는 p의 필요조건
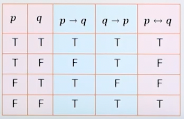
쌍조건명제(conditional proposition, ↔)
명제 p와 q가 있을 때, 명제 p와 q가 조건의 역할과 결론의 역할을 동시에 수행하는 경우
p ↔ q
(p → q)^(q → p)
동치
논리적 동치(logical equivalence, ≡)
두 명제 p와 q가 논리적으로 동등하면 논리적 동치라고 한다.
두 명제가 항상 동일한 진리값을 가진다는 의미
역, 이, 대우
- 조건명제 p → q
- 역(converse) : q → p
- 이(inverse) : ~p → ~q
- 대우(contrapositive) : ~q → ~p

논리적 동치법칙
1) 교환법칙(commutation law)
2) 결합법칙(associative law)
3) 분배법칙(distrivutive law)
4) 항등법칙(identity law)
5) 지배법칙(domination law)
6) 부정법칙(negation law)
7) 이중 부정법칙(double negation law)
8) 멱등법칙(idempotent law)
9) 드 모르간 법칙(de Morgan's law)
항진명제(tautology) : 항상 참인 명제
모순명제(contradiction) : 항상 거짓인 명제
✔ 술어논리와 명제함수
논리(logic)
명제논리(proposition logic)
- 명제
술어논리(predicate logic)
- 명제함수
x + 2 = 0
명제함수(proposition funcion)
변수의 값에 의해 함수의 진리값이 결정되는 문장이나 식
- 변수의 명세 : 변수의 값을 적시
- 변수의 범위를 제시 (한정화; ∀)
한정화(quantification)
전체한정자(universal quantifier, ∀) : "모든" 또는 "임의의" 를 의미
명제함수 ∀𝑥P(𝑥)와 같이 사용되었을 경우 정의역의 모든 임의의 𝑥에 대해서 P(𝑥)가 참(T)임을 의미한다.
존재한정자(existential quantifier, Ǝ) : "존재한다" 를 의미
명제함수 Ǝ∀𝑥P(𝑥)와 같이 사용되었을 경우 정의역의 어떤 𝑥에 대해서 P(𝑥)가 참(T)임을 의미한다.
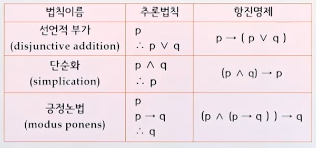
✔ 추론
추론(inference) : 참으로 알려진 명제를 기초로 다른 명제를 유도해내는 과정
유효추론
전제를 참이라고 가정하였을 때 결론이 항상 참이 되는 추론
추론규칙
기본적인 추론규칙은 논리적 동치(항진명제)를 이용한다.